Curve-Fitting

Ron Averill 0 Comments

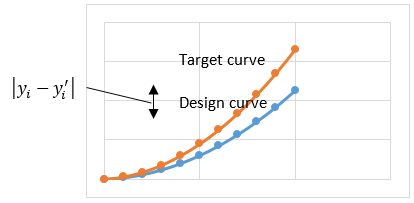
We often need for a design or a model to perform in a specified way. For example, the parameters in a nonlinear material model should be selected to best match the experimental stress-strain response. The geometrical parameters of a rubber bushing should be designed so that its force-deflection response matches the desired nonlinear stiffness behavior.

Optimization problems like these arise frequently. We refer to them as curve-fitting problems, because the goal is to minimize the difference between the specified target curve and the actual response curve
of our design or model.

Figure 1.

Figure 1. The difference between a target curve and a design curve is minimized in a curve fitting optimization problem.

Continue reading →

Reducing the Accidental Coupling of Variables

Ron Averill 0 Comments

One of the challenges to finding optimal solutions is the coupling of variables. If we could change one variable at a time, the search process would be so much easier. But in most problems the variables are strongly coupled, so the best value for one variable depends on the values of many other variables.2variables

Often, we have no control over this variable coupling, since it is inherent in the physics model that defines our objectives and constraints. In these cases, we need a powerful optimization search strategy like SHERPA to figure out the complexities of the design landscape and to produce an optimized solution.

But in some cases we make this task harder than it needs to be because of how we represent the problem. That is, sometimes the way we define the problem creates unnecessary coupling or increases the complexity of existing coupling among variables. This makes the optimization search harder, and may decrease the chance of finding the optimal solution within our limited optimization search budget. The good news is that we can often alleviate this situation with a different representation.  Continue reading →

HEEDS MDO 2015: Compute Resources Set

Ranny Sidhu 0 Comments

This new feature provides the ability to treat multiple computer resources as a single resource, without a job queuing system, to parallelize your HEEDS study. It allows for tremendous flexibility in the use and management of disparate computer resources.

As the name suggests, a compute resource set is a set of previously defined compute resources in HEEDS. The set allows you to define a pool of hardware resources that can be used to parallelize one or more analyses in the HEEDS study. The definition is not limited to homogeneous resources but can include any type of compute resource available. For example, a resource set could be a set of Windows workstations (as shown in the example image below), a set of Windows and Linux workstations, some workstations along with a cluster, several different clusters, etc. During the run, HEEDS will manage the job submissions to the resources defined in the set to make sure they are used effectively.  Continue reading →

HEEDS MDO 2015: Logic in Process Definition

Ranny Sidhu 0 Comments

LogicThe process definition now provides support for the use of logic to drive the flow in the analysis process. One or more conditions can be defined at the analysis level to control whether an analysis will be attempted. Several scenarios that would have required specialized external scripts to capture the desired process behavior are now easily handled with this feature. Some of these scenarios are listed below:

  • Improve efficiency in the evaluation process by skipping compute intensive analyses when it is clear that the design would not be acceptable
  • Continue execution of the process even when some of the analyses result in errors
  • Use of an appropriate physics model based on the results of an upstream analysis  Continue reading →

Optimizing the Number and Location of Design Features (without using a CAD model)

Ron Averill 0 Comments

Recent advances in process automation and optimization search technology have made it easier than ever to perform automated design studies and discover innovative solutions. But we still have to define the problem we want to solve and then decide how to represent that problem in our models. These two tasks are sometimes challenging, and they rely heavily on experience and intuition. In this article, as well as some future ones, we will share some of our experience in defining and representing various types of optimization problems. Hopefully you will find some of these techniques useful in your applications.

Numbers and locationsA common design scenario is to optimize the number and location of certain design features to satisfy performance goals and requirements. For the sake of discussion, let’s consider a specific example of this type of problem. Continue reading →

Welcome

admin 0 Comments

Welcome to the HEEDS Design Space Exploration Blog, your trusted source for education and conversation about Design Space Exploration and HEEDS. From classical algorithms to modern techniques, structural methods to multidisciplinary strategies, and simple tutorials to advanced commercial applications, we provide the information you need to successfully apply design space exploration to virtually any problem. Discover Better Designs, Faster!

Series Hybrid vs. Parallel Hybrid

Ron Averill 0 Comments

Hybrid refers to something that is made up of two or more diverse ingredients. The goal in combining them is to capture and merge the advantages of each ingredient, while overcoming any disadvantages. But ingredients can be combined in many ways, resulting in considerable variation in performance depending on how they are combined.

In optimization search algorithms, as with electric vehicles, there are two main categories of hybrids: series and parallel. To better understand the basic differences between the series and parallel hybrid approaches, let’s consider a simple illustration.
Continue reading →