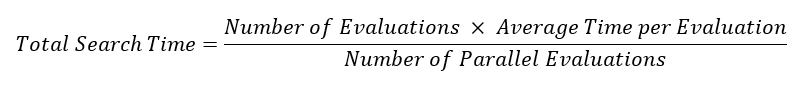Welcome to the HEEDS Design Space Exploration Blog, your trusted source for education and conversation about Design Space Exploration and HEEDS. From classical algorithms to modern techniques, structural methods to multidisciplinary strategies, and simple tutorials to advanced commercial applications, we provide the information you need to successfully apply design space exploration to virtually any problem. Discover Better Designs, Faster!
Simcenter SPEED – Rapid Electric Machine Design Software
Simcenter SPEED is an all-in-one specialized tool for the sizing and preliminary design of electric machines such as motors, generators and alternators. This software provides a built-in graphical user interface to access HEEDS in two ways: as a full HEEDS installation and as an integrated add-on tool. HEEDS enables Simcenter SPEED to automate and intelligently explore the design space resulting in increased machine efficiency at a lower cost.
Combined with STAR-CCM+, Simcenter SPEED offers design engineers a unique and powerful ability to model electromagnetic and flow/thermal capabilities in the same working process. This results in an end-to-end multiphysics solution for electric machine design and allows for thermal and stress management under a wide range of environmental conditions, leading to more affordable and better performing electric machines.
Simcenter SPEED benefits and features at a glance:
- Electric machine template: set-up an electric machine model in minutes
- Multi-physic software link: seamless import to Finite Element software
- Design space exploration: automatically optimize electric machine performance with HEEDS
- System level simulation: model export to system level model within Simcenter Amesim
Download the Simcenter SPEED fact sheet
Download the Simcenter SPEED Rapid Electric Machine Design Spotlight
Read more about Simcenter SPEED here
New Release HEEDS 2018.10
HEEDS 2018.10 is full of new upgrades to make your experience more flexible and more intuitive than ever before. Improved usability and simplification of analysis set up will allow for all design project team members to easily deploy HEEDS. With four new major portals added, HEEDS continues to find new ways to work with your existing software investments. HEEDS 2018.10 is packed with great enhancements that continue to streamline design space exploration through improved results, processing, and automated analysis tools.
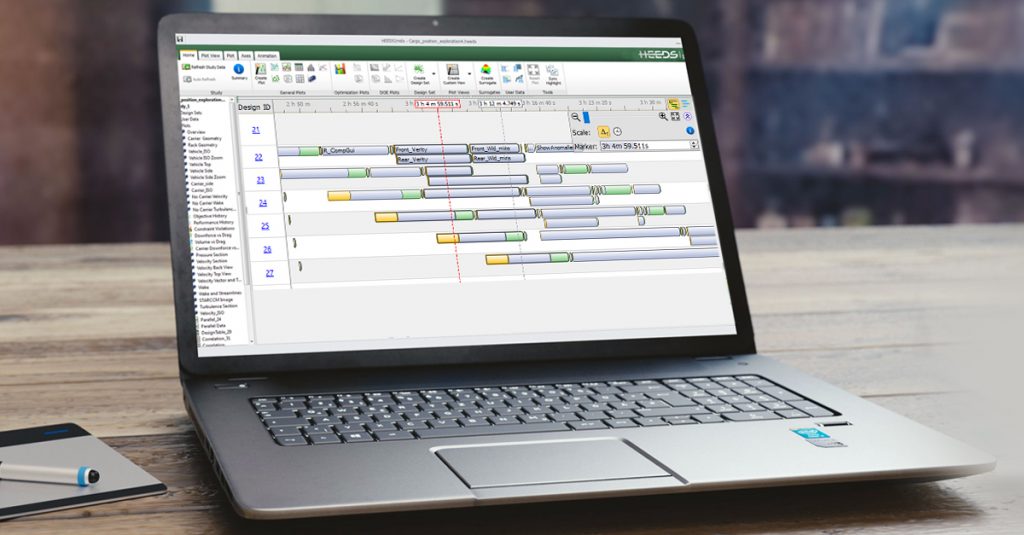ANALYSIS TIME VIEW
It can be difficult to assess the process status when analyses are running with complex or parallel processes in HEEDS|MDO. The analyses’ execution stages can now be easily visualized in a Gantt-like time scale view allowing investigation of execution conflicts and bottlenecks.
COMPUTE RESOURCE SPECIFIC PORTAL PROPERTIES
Software is often installed at different locations on different machines accessed by HEEDS|MDO, making it challenging to set up an analysis with the proper execution command that works on all systems. HEEDS 2018.10 is now equipped with a simple and powerful uniform interface that allows you to specify, for each compute resource, the right configuration properties to run your solvers on that particular system, time and again, without having to reconfigure to accommodate other systems.
STUDY RELATIONSHIPS
There are design problems that require input variable equality constraints to be enforced, which can be cumbersome to formalize into an optimization problem statement. With this new feature, ensuring the design variables add-up to a specific value is now easier than ever.
FOUR NEW PORTALS: FEMAP, FLOMASTER, FLOTHERM AND SAMCEF
With new major portals being added, such as FEMAP, Samcef, FloMASTER and FloTHERM, HEEDS continues to find new ways to help you leverage your software investments. HEEDS 2018.10 also is packed with improvements to existing portals to boost productivity.
XML TAGGING
The new version of HEEDS now fully supports parsing XML files for tagging. Use this feature to tag, auto-tag and multi-tag input and output parameters. Tagging with XML is easy to use and requires no prior XML knowledge.
IMPROVED USER DATA HANDLING
We’ve seen our users manage a lot of external data sets. They are often willing to import them into HEEDS for post processing and optimization. Now we’ve made the experience much easier and straightforward by allowing the seamless import of external data sources into HEEDS with a single button push! You can also use this feature to plot data from multiple studies on the same plot.
To download HEEDS MDO 2018.10, log into your Customer Portal account or go to the Siemens Global Technical Access Center .The newest Release Notes are also available for download on both sites. Visit redcedartech.com for more information on how HEEDS can drive innovation and success within your company.
HEEDS MDO 2018.04 Release
Siemens PLM provides powerful tools for quickly and easily exploring product design options to discover the best possible designs to meet your needs. HEEDS 2018.04 is packed with great enhancements that continue to streamline design space exploration through improved results processing, increased environment flexibility, streamlined workflow definition, automation of analysis tool capture.
Some Highlights:
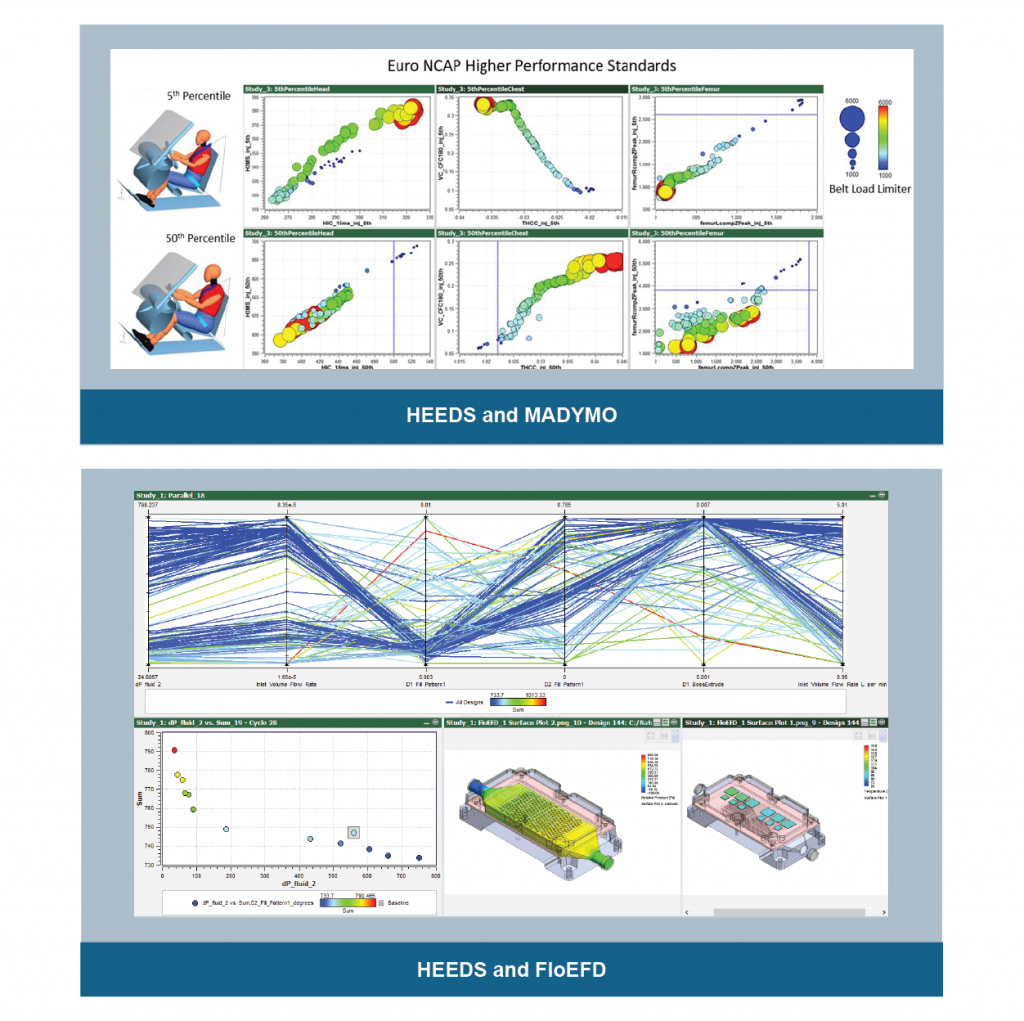
- New Portals – Easily include AVL DVI (Cruise), FloEFD, Fluent, MADYMO, and System Synthesis models within your workflow
- Parameter Groups – Organize parameter data into custom groups to easily manage large projects
- Analysis Environment Data – Customize the environment needed for each analysis without the need for scripting
- Vector Response Plot – Create 2D/3D curve plots from vector responses with the User Plot
- Non-Dominated Sorting Tool – Evaluate trade-offs between responses in HEEDS Post for all study types
- Surrogate Sensitivities Plot – Interrogate local sensitivities to better understand trends
To download HEEDS MDO 2018.04, go to your Customer Portal account or to the Siemens Global Technical Access Center. The newest Release Notes are also available for download on both sites.
|
|
Collaborative Design Exploration
Intuition plays a critical role in all stages of a design exploration study, from defining the problem statement to building the simulation model to interpreting the results. But what about the search process itself? Should we make design improvements based on intuition, or should we allow a mathematical search engine to explore the design space for better designs? The answer is both. We call this shared process collaborative design exploration.
The SHERPA search strategy allows you to inject your design ideas before and during an exploration study. Before you start a study, you can seed it with multiple ideas (in the form of actual designs) that might help SHERPA to locate productive regions of the design space more quickly, thus speeding up the overall search. For example, in addition to the baseline design, you might consider seeding the study with other potentially good designs that:
you have investigated or produced in the past- your competitors have used
- are feasible, but perhaps not optimal
- are high performing relative to one or more criteria, but not all of them
- have some desirable features, but don’t necessarily perform well
- you have a hunch may work well
- are from a previous HEEDS MDO study
One or more of these injected ideas might contribute to a more efficient search, while the cost of doing this is only the time to enter the variable values that define each of the designs. SHERPA will evaluate the injected designs when the search process is launched, so there is no need to simulate them before injection. Continue reading
Using Design Sensitivities
Design sensitivities are a measure of how much an objective or constraint response varies due to a small change in a design variable. Based on this definition, they are sometimes referred to as sensitivity derivatives. Let’s discuss how to use them properly, as well as how not to use them.
First, note that the design sensitivities we refer to here are calculated for a particular design, not for a design space. Statistical methods of sensitivity analysis can provide useful information about a design space, but not the type of information we seek here.
Since a design represents a point in the design space, it is clear that sensitivities are defined at a point, as are mathematical derivatives. Two distinct designs within a design space will probably have different sensitivities unless the design space is linear, which is seldom the case for engineering problems. Continue reading
Service That Customers Truly Want and Need
I received an email today from a marketing organization that began with the question: “What if the next time a customer came through your door, they could interact with a hologram speaking their own language. Your company would look pretty innovative and well, just straight up cool.”
If you’re anything like me, you’ve had your fill of speaking to robotic phone operators or pushing fifteen buttons on your phone to get routed to someone who has any chance of actually helping you with your question or challenge. Don’t get me wrong, I love new and innovative technology. But, only if it really helps me do things faster, easier, or better. Continue reading
How to Accelerate Your Design Exploration Studies
We all feel the “need for speed” when trying to find better design solutions through simulation. What can we do to speed up our design exploration studies? Let’s discuss all the options here, including one that may not be obvious.
In a typical study, the total CPU time needed to perform a design exploration study is determined using this simple formula:
HEEDS Analysis Templates
The first step in any design exploration study is to define the way in which the virtual prototype simulation model is to be constructed and modified. This typically involves identifying the various modeling and simulation tools that are involved, specifying where they are executed, choosing the simulation models that are being modified, selecting the parameters being driven and monitored, and documenting what outputs are being stored for each design point.
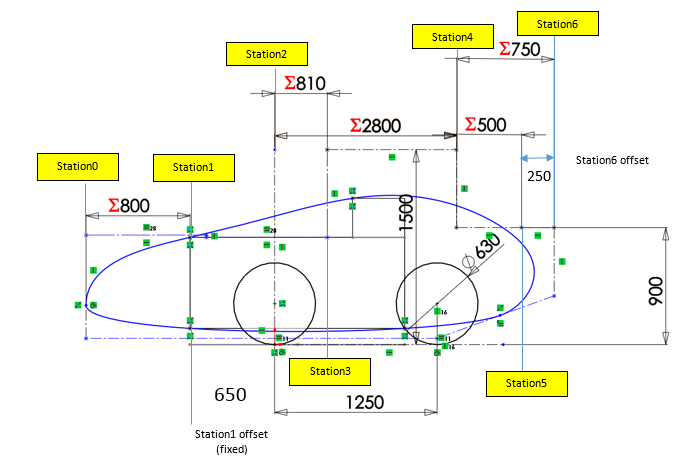
While the actual simulation models may change from project to project, the workflow and the way the models are tested often remains the same. For example, the workflow for finding the best lower control arm configuration for a vehicle front suspension is identical (or very similar) across vehicle platforms. The input for geometry ranges, loads and required performance change.
Figure 1. Example HEEDS workflow
Exploring Design Performance Relationships
Highlighting a Few New Features that Help You Discover Better Designs, Faster
Often, improvements to the simplest things can have a big impact on your daily tasks. There are many tasks we perform repeatedly when working with HEEDS, and streamlining those saves time and reduces effort. HEEDS 2015.11 contains many enhancements focused on simplifying workflows and I want to highlight a few that help in exploring design performance relationships.
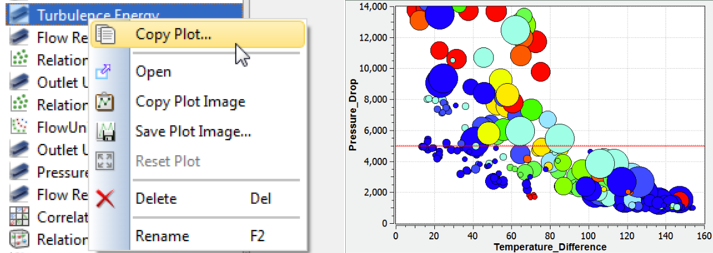
To explore relationships between variables and responses in detail, you typically require multiple plots of the same type, but with different variables to gain a clearer understanding of dependency or influence. However, there are many plot features that are tailored to suit the particular way you want to view the results such as axis scales, data symbols, curves styles, title fonts, and so on.
To avoid having to create a new plot from scratch and redefine all these settings, you can now right click and select the Copy Plot option. This makes an exact copy of the existing plot, with all the customization. You then just need to alter the variables or responses being displayed saving a lot of setup time.
Figure 1. Make a copy of an existing plot with a single right click option
Thinking in Parallel
There are a lot of great tools in HEEDS to help you gain insight into finding the best design. One area of enhancements in HEEDS 2015.11 focused on parallel plots. In this article, we’ll highlight some ways to use new features of parallel plots in HEEDS to discover better designs, faster.
Parallel plot background
To help show the new capabilities in the context of an engineering problem, let’s look at exploring shape options for a human powered vehicle. There are obviously many dimensions that can be adjusted to improve the design.
Figure 1. Possible parameters to change for a Human Powered Vehicle