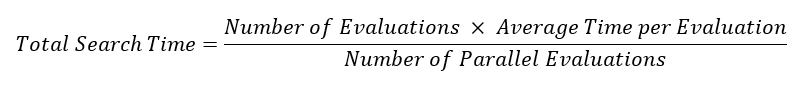Intuition plays a critical role in all stages of a design exploration study, from defining the problem statement to building the simulation model to interpreting the results. But what about the search process itself? Should we make design improvements based on intuition, or should we allow a mathematical search engine to explore the design space for better designs? The answer is both. We call this shared process collaborative design exploration.
The SHERPA search strategy allows you to inject your design ideas before and during an exploration study. Before you start a study, you can seed it with multiple ideas (in the form of actual designs) that might help SHERPA to locate productive regions of the design space more quickly, thus speeding up the overall search. For example, in addition to the baseline design, you might consider seeding the study with other potentially good designs that:
 you have investigated or produced in the past
you have investigated or produced in the past- your competitors have used
- are feasible, but perhaps not optimal
- are high performing relative to one or more criteria, but not all of them
- have some desirable features, but don’t necessarily perform well
- you have a hunch may work well
- are from a previous HEEDS MDO study
One or more of these injected ideas might contribute to a more efficient search, while the cost of doing this is only the time to enter the variable values that define each of the designs. SHERPA will evaluate the injected designs when the search process is launched, so there is no need to simulate them before injection. Continue reading